Why Do We Use Learning Rate Warm-Up in Deep Learning?

Training deep neural networks is notoriously sensitive to hyperparameters, especially the learning rate. One widely adopted technique to improve stability and performance is learning rate warm-up. But why does warm-up help, what exactly does it do and the effect of Warm-up duration and how does it behave with different optimizers like SGD and Adam?

What Is Learning Rate Warm-Up?

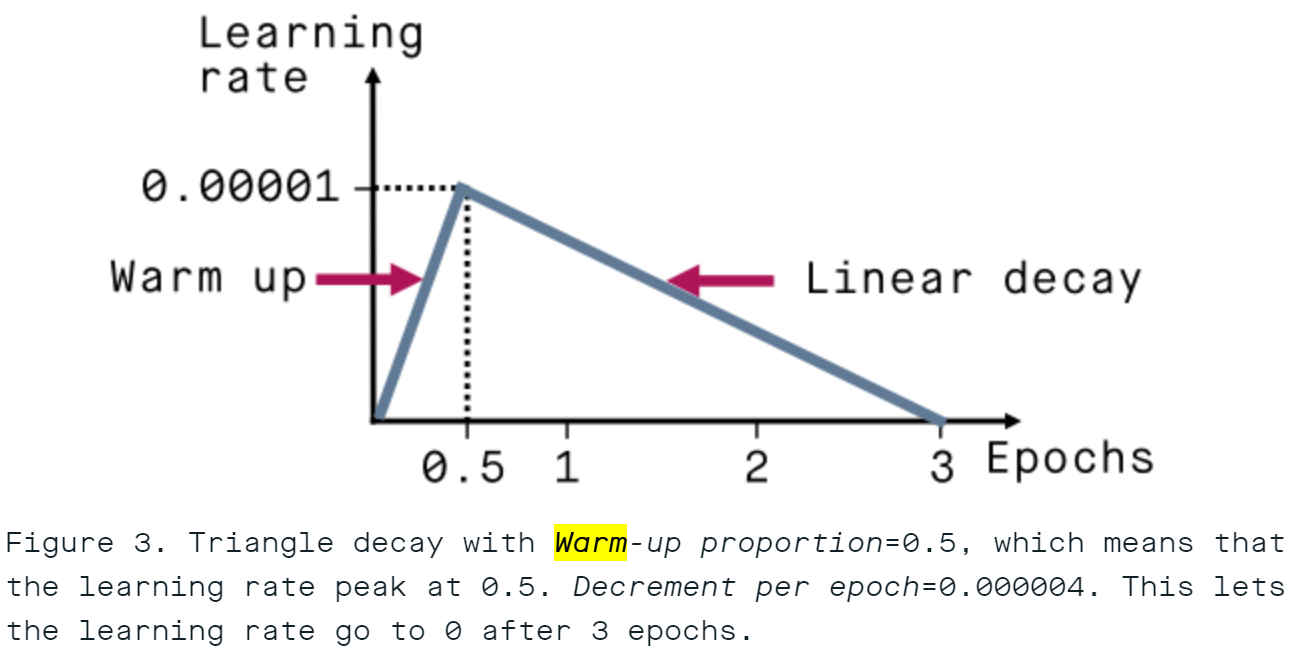
Learning rate warm-up is a simple technique where the learning rate starts small and gradually increases to a target value over a few iterations or epochs.

Example:

If your target learning rate is 1e-4, instead of starting training with 1e-4 immediately, you might increase the learning rate gradually smaller value (e.g., 1e-6) to 1e-4 over the first 5 epochs the first 5 epochs this is known as the warm-up period (or warm-up steps if measured in iterations).

PyTorch Code Example

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

import math
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader, TensorDataset
from torch.optim.lr_scheduler import LambdaLR

# Config
base_lr = 1e-4
warmup_epochs = 5
total_epochs = 20
batch_size = 512
steps_per_epoch = 1000 // batch_size  # dataset size / batch size
total_steps = total_epochs * steps_per_epoch
warmup_steps = warmup_epochs * steps_per_epoch

# Dummy data and model
X, y = torch.randn(1000, 10), torch.randint(0, 2, (1000,))
loader = DataLoader(TensorDataset(X, y), batch_size=batch_size, shuffle=True)
model = nn.Sequential(nn.Linear(10, 64), nn.ReLU(), nn.Linear(64, 2))
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=base_lr)

# Cosine warm-up scheduler
def get_cosine_schedule_with_warmup(optimizer, num_warmup_steps, num_training_steps):
        """
        Create a schedule with a learning rate that decreases following the values of the cosine function
        between the initial lr set in the optimizer to 0, after a warmup period during which it increases
        linearly between 0 and the initial lr set in the optimizer.
        """
        def lr_lambda(current_step):
            if current_step < num_warmup_steps:
                return float(current_step) / float(max(1, num_warmup_steps))
            progress = float(current_step - num_warmup_steps) / float(max(1, num_training_steps - num_warmup_steps))
            return max(0.0, 0.5 * (1.0 + math.cos(math.pi * progress)))
        
        return LambdaLR(optimizer, lr_lambda)

# ---- Scheduler ----
scheduler = get_cosine_schedule_with_warmup(optimizer, num_warmup_steps=warmup_steps, num_training_steps=total_steps)
lrs = []

# Training loop
for epoch in range(total_epochs):
    model.train()
    total_loss = 0

    for xb, yb in loader:
        optimizer.zero_grad()
        loss = criterion(model(xb), yb)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()

    scheduler.step()  # Update learning rate based on current epoch

    lrs.append(optimizer.param_groups[0]['lr'])
    print(f"Epoch {epoch+1:2d}, LR: {lrs[-1]:.4f}, Loss: {total_loss / len(loader):.4f}")

Visualize the Learning Rate Schedule

⚠️ Problem Without Warm-Up: Unstable Gradients

At the start of training, neural networks often have randomly initialized weights. Applying the gradient steps at the beginning of training are not meaningful, and thus it would be harmful to take large steps in such directions, especially when:

• The gradients are sharp they change rapidly with respect to input.
• The loss landscape is highly curved in certain directions.

This can cause exploding gradients, oscillations, or divergence.

Also training instabilities, often referred to as ‘catapults’ arises when the learning rate $\eta$ exceeds a critical threshold $\eta_c$, i.e.,

$$ \eta > \eta_c(t) $$

Two behaviors follow:

• Mild Overshoot: If $\eta_c < \eta < \eta_{\max}$, training becomes temporarily unstable but self-stabilizes during training.
• Severe Overshoot: If $\eta > \eta_{\max}$, training suffers catastrophic divergence, sometimes called a catapult effect.

Warm-Up Reduces Gradient Sharpness

What is Sharpness?

Sharpness refers to how rapidly the loss changes in different directions in weight space. Mathematically, it’s related to the Maximum eigenvalue of the Hessian (second derivative matrix of the loss): :

$$ \lambda_H(t) := \lambda_{\text{max}}(\nabla^2_\theta \mathcal{L}) $$

• Sharp gradient = large Hessian eigenvalues
• High sharpness implies instability with large learning rates.

Effect of Warm-Up (Warm-Up as a Stabilizer):

Warm-up reduces gradient sharpness early in training. As a result, the network:

• Learns smoother, more stable gradients
• Becomes more robust to the final large learning rate after warm-up
• Avoids divergence in early epochs

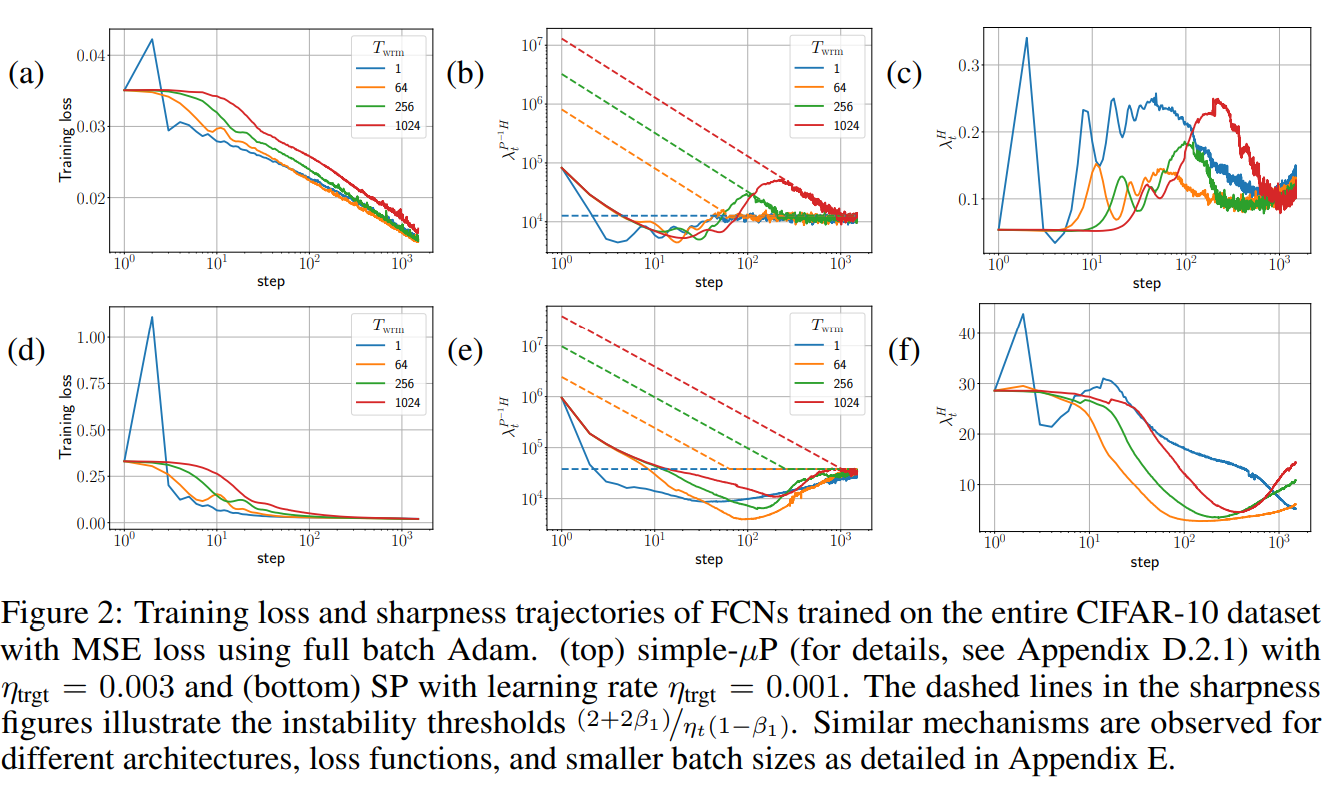
• At that subplot (a), (d) loss decreases more smoothly (indicating more stable network).

• At that subplot (c), (f) that $\lambda^H$ (Largest eigenvalue of Hessian) are more smoother (indicating loss sharpness across lose curvature).

• Long warm-up (bigger $T_{wrm}$) delays aggressive learning, letting model “adapt its curvature” first.

Warm-up acts as a step that brings the network into a “safe zone” of the loss landscape where sharpness is lower and training is more stable.

Warm-Up Allows Higher Learning Rates

Learning rate grows slowly, avoiding premature crossing of $\eta_c$. Gives network time to smooth the loss surface. prepares the network to tolerate a higher learning rate after the warm-up phase.

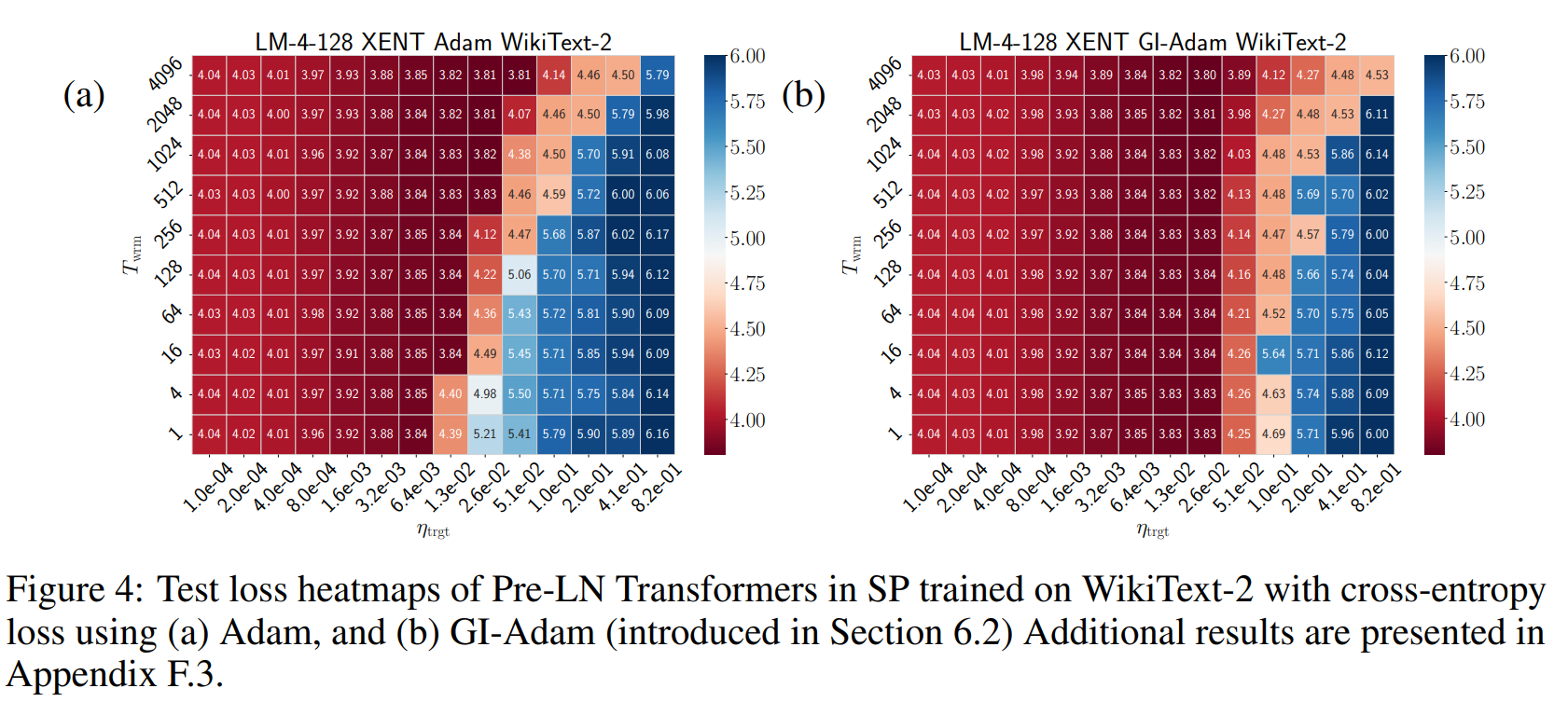
In Figure, the authors measure test loss across combinations of:

• Target learning rate $\eta_{\text{trgt}}$
• Warm-up duration $T_{\text{warm}}$

Two optimizers are compared:

• (a) Adam
• (b) GI-Adam (gradient injection variant)

Observations:

• With short warm-up durations, high learning rates lead to catastrophic loss explosions (deep blue areas).

• Longer warm-ups shift the safe zone rightward → allowing higher learning rates without divergence.

• This suggest that warm-up extends the stability region in the $(\eta_{\text{trgt}}, T_{\text{warm}})$ space.

Key Finding:

Longer warm-up leads to more reduction in sharpness, and therefore even larger learning rates can be used safely.

Why is this important?

• Large learning rates speed up training by taking bigger steps (less time - less compute).
• Less time speed for hyperparameter tuning.

⚖️ Warm-Up in Adam vs. SGD: What’s the Difference?

Warm-up benefits both SGD and Adam, but in different ways:

Warm-Up + Adam:

• The adaptive optimizers such as Adam argues that the variance of the adaptive learning rate is large during early training because the network has seen too few training samples.

• Warmup acts as a variance reduction method by allowing the network to collect accurate statistics of the gradient moments before using larger learning rates.

Warm-Up + SGD:

• SGD is more sensitive to sharpness because it lacks adaptive scaling.
• Warm-up has a strong effect on SGD’s stability and learning rate tolerance.
• Without warm-up, SGD can easily diverge at high learning rates.

Both optimizers show improved stability and performance with warm-up, but the benefit is more critical for Adaptive optimizers.

TL;DR - Warm-Up Effects in Training

📚 References

• “Underlying Mechanisms Behind Learning Rate Warmup’s Success”
• “A Theoretical Understanding of Learning Rate Warmup in Deep Learning”